


Sayama, "Life Worth Mentioning: Complexity in Life-Like Cellular Automata," Artificial Life, 27(2), 2021 pp.

The reason it is called a game is because people who play the game can set it up in different ways to make it do different things. Any outer-totalistic, two-state, two-dimensional Life-like rule may be simulated with this Demonstration. The Game of Life is an imaginary robot game ( cellular automaton) made by the British mathematician John Horton Conway in 1970. For example, Conway's Game of Life is written as in this notation. The and are subsets of digits from 0 to 8 that represent the number of live neighboring cells in a Moore neighborhood that would either birth a cell from being dead or allow a live cell to survive, respectively. This refers to the analogy of cells being dead (0 or white) or alive (1 or black). in Haskell see also Shortest game of life. My implementation worked by keeping 2 arrays of booleans, representing the last state, and the state being updated (the 2 arrays being swapped at each iteration). So congrats if you came up with it by yourself If youre looking for smart implementations I would recommend functional ones, e.g. To experiment, Ive (long ago) implemented Conways Game of Life (and Im aware of this related question). One of the most important distinguishing characteristics of Conway's Game of Life is that. Any live cell with more than three live neighbours dies. Each square (or 'cell') on the grid can be either alive or dead, and they evolve according to the following rules: Any live cell with fewer than two live neighbours dies (referred to as underpopulation). The stands for birth and the stands for survival. First of all, I think the algorithm is pretty smart which is, for my humble experience, not so common for a college student. RULE VARIATIONS two neighbors is empty, it will remain empty. Conway's Game of Life is a cellular automaton that is played on a 2D square grid. Before you start the game, you need to provide an initial state. A cell can either be dead or alive (alive cells are coloured blue in our demo). The rules are as follows: Each cell lives in a square in a rectangular grid. The convenient naming convention is used to refer to various rules for two-dimensional outer-totalistic CAs. Conways Game of Life is a game invented by mathematician John Conway in 1970. Life has inspired an entire category of CA rules referred to as Life-like rules-rules that behave similarly to Life. The glider is a pattern that travels across the board in Conways Game of Life. The c/4 period is clearly visible as 'stacks' of cells that remain alive for successive generations. A three-dimensional view of a glider, with previous generations visible going down the z-axis. Live cells with exactly two or three live neighbors survive. Glider (Conways Life) The mutation and movement of a 'glider'. Being surrounded by exactly three live neighbors turns a dead cell (state 0) into a live cell.Ģ. Live cells (cells in state 1) with too few live neighbors die from isolation, whereas those with too many live neighbors die from suffocation.ġ. In 1970, English mathematician John Horton Conway, after experimenting with various CA rules, settled on Life, which incorporated analogies to real living organisms-with births, deaths and survival in the natural world. cgol.The cellular automaton (CA) rule that has gained the most popularity by far is Conway's Game of Life.
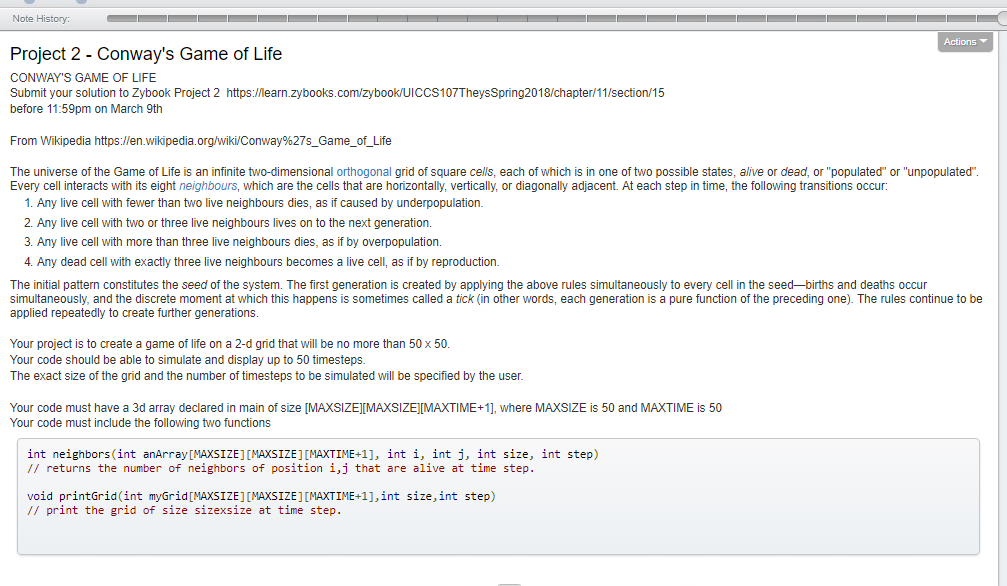
VARIATIONS OF CONWAYS GAME OF LIFE CODE
cgol.js - the actual JavaScript code logic that runs and updates grid universe with the Game of Life and other simulation games.Pick a desired ruleset from the dropdown or put in your own ruleset! Choose the population density, desired FPS, colors, and click 'restart simulation' to start simulation using your desired parameters. Some interesting rule-sets are supported via drop-down select by default. Conways Game of Life is a cellular automaton that was devised in the 1970s by a British mathematician named, well, John Conway. Thus, Conway's Game of Life can be described as B3/S23 using this format. Where X is the number of neighbors required for an empty cell to be 'born' in a location, while Y is the number of neighbors required for a living cell to continue living.


 0 kommentar(er)
0 kommentar(er)
